Educational Codeforces Round 112 (Rated for Div. 2)
https://codeforces.com/contest/1555
C. Coin Rows
题意:
两行数,第一个人先走,拿走所有经过的;第二个人再走。只能往右下走,从左上出发。第一个人想让第二个拿的最少,第二个人要拿的最多,问第二个人拿多少
做法:
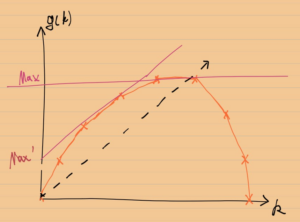
推一下发现是第二层的前缀和与第一层后缀和取max
拓展:
不妨考虑一下若不止两行该怎么做
D. Say No to Palindromes
题意:
给一个由abc三个字母组成的串,问至少改几个字母使得每个子串均不为长度大于1的回文。每次询问原串的一个子串
做法:
观察可知条件等价为连续三个字符各不相同,共六种情况,枚举即可,答案满足可加性
E. Boring Segments
题意:
数轴上给若干条线段,给出左右端点及其权值。当选取一条线段时,其覆盖的所有整点“连通”。现要求选定一个子集,使全部整点连通,同时使得最大权值减最小权值最小
做法:
首先,“连通”条件可进行转化:所有整点“连通”等价为所有整点及半整点 (x.5) 均被覆盖
由此,可以利用线段树对整体连通性进行维护:将点数翻倍(加上半整点),添加线段即区间 +1,移除即区间 -1,若全局最小值大于 0 则为连通
基于此,不难想到另一部分,将线段按权值从小到大排序,用 2-pointer 就能 O(n) 枚举所有情况
总复杂度 O(nlogn)
AC代码
#include <algorithm>
#include <iostream>
using namespace std;
const int MAX_N = 3E5 + 100;
const int MAX_M = 2E6 + 100;
const int INF = 1E6 + 100;
class SegmentTree {
private:
int n;
int a[MAX_M << 2], lz[MAX_M << 2];
void modify(int n, int l, int r, int ll, int rr, int x) {
if (ll <= l && r <= rr) {
a[n] += x;
lz[n] += x;
return;
}
int mid = (l + r) >> 1;
if (lz[n]) {
modify(n << 1, l, mid, l, mid, lz[n]);
modify(n << 1 | 1, mid + 1, r, mid + 1, r, lz[n]);
lz[n] = 0;
}
if (ll <= mid) modify(n << 1, l, mid, ll, rr, x);
if (mid < rr) modify(n << 1 | 1, mid + 1, r, ll, rr, x);
a[n] = min(a[n << 1], a[n << 1 | 1]);
}
public:
void init(int _n) { n = _n; }
void modify(int l, int r, int x) { modify(1, 1, n, l, r, x); }
bool query() { return a[1]; }
};
class Segment {
public:
int l, r, w;
bool operator<(const Segment& s) { return w < s.w; }
};
int n, m;
SegmentTree tr;
Segment seg[MAX_N];
int main() {
ios::sync_with_stdio(false);
cin >> n >> m;
for (int i = 0; i < n; ++i) {
cin >> seg[i].l >> seg[i].r >> seg[i].w;
seg[i].l = seg[i].l * 2 - 1;
seg[i].r = seg[i].r * 2 - 1;
}
sort(seg, seg + n);
tr.init(2 * m - 1);
// init
int ans = INF;
int l = 0, r = -1;
while (!tr.query()) {
r += 1;
tr.modify(seg[r].l, seg[r].r, 1);
}
while (l < n) {
if (tr.query()) ans = min(ans, seg[r].w - seg[l].w);
tr.modify(seg[l].l, seg[l].r, -1);
l += 1;
while (r + 1 < n && !tr.query()) {
r += 1;
tr.modify(seg[r].l, seg[r].r, 1);
}
}
cout << ans << endl;
return 0;
}心路历程:
折磨了一个多小时没想出来,最后看的题解
2-pointer倒不难想,维护这样的权值模式排序后这么扫比较常见
维护是完全没想到,一直在考虑dp线段树优化,最关键的第一步转化还是第一次见,是一个好技巧
F. Good Graph
题意:
动态维护一个图,只有加边操作。需要满足加边后任一简单环上异或和为 1,否则添加失败
做法:
首先观察出下面几个性质
- 若添加前两端点不连通,则添加成功
- 若添加的两端点在一棵树上,则路径异或和为 1 时添加成功
- 若添加的两点已经在一个简单环上,添加必失败
- 若添加的两端点间原路径有任一段包含在任一环上,添加必失败
后两条性质整合一下就是当添加的两端点间的路径经过一条环的边的话,必失败
然后就结束了,这显然用LCT维护就好了
需要注意的是IO量比较大,需要快读
AC代码
#include <cstdio>
#include <utility>
using namespace std;
const int MAX_N = 3E5 + 100;
class Node {
public:
int val, tot;
bool isEdge;
int eSz;
int flag, flz, fTot;
bool flip;
Node *c[2], *p, *pp;
void fix() {
tot = val;
fTot = flag;
eSz = isEdge;
if (c[0]) {
c[0]->p = this;
tot ^= c[0]->tot;
fTot += c[0]->fTot;
eSz += c[0]->eSz;
}
if (c[1]) {
c[1]->p = this;
tot ^= c[1]->tot;
fTot += c[1]->fTot;
eSz += c[1]->eSz;
}
}
void pushFlip() {
if (flz) {
flz = 0;
flag = isEdge;
if (c[0]) {
c[0]->flz = 1;
c[0]->fTot = c[0]->eSz;
}
if (c[1]) {
c[1]->flz = 1;
c[1]->fTot = c[1]->eSz;
}
}
if (!flip) return;
flip = 0;
swap(c[0], c[1]);
if (c[0]) c[0]->flip ^= 1;
if (c[1]) c[1]->flip ^= 1;
}
int type() { return p ? this == p->c[1] : 2; }
void rot(int i, int j) {
bool b = i ^ j;
Node *x = c[i], *y = 2 == j ? x : x->c[j], *z = b ? y : x;
if (y->p = p) p->c[type()] = y;
c[i] = z->c[i ^ 1];
if (j < 2) {
x->c[j] = y->c[j ^ 1];
z->c[j ^ 1] = b ? x : this;
}
y->c[i ^ 1] = b ? this : x;
fix();
x->fix();
y->fix();
swap(pp, y->pp);
}
void splay() {
for (pushFlip(); p;) {
if (p->p) p->p->pushFlip();
p->pushFlip();
pushFlip();
if (2 == p->type())
p->rot(type(), 2);
else
p->p->rot(p->type(), type());
}
}
Node *first() {
pushFlip();
return c[0] ? c[0]->first() : (splay(), this);
}
};
class LCT {
public:
Node node[MAX_N << 1];
Node *access(Node *u) {
for (u->splay(); Node *pp = u->pp; u = pp) {
pp->splay();
u->pp = 0;
if (pp->c[1]) {
pp->c[1]->p = 0;
pp->c[1]->pp = pp;
}
pp->c[1] = u;
pp->fix();
}
return u;
}
void makeRoot(Node *u) {
access(u);
u->splay();
if (u->c[0]) {
u->c[0]->flip ^= 1;
u->c[0]->p = 0;
u->c[0]->pp = u;
u->c[0] = 0;
u->fix();
}
}
bool connected(Node *u, Node *v) {
Node *ru = access(u)->first();
return ru == access(v)->first();
}
void link(Node *u, Node *v) {
if (connected(u, v)) return;
makeRoot(u);
u->pp = v;
}
void cut(Node *u, Node *v) {
makeRoot(v);
u->splay();
if (v != (u->pp ?: u->c[0])) return;
if (u->pp) {
u->pp = 0;
} else {
u->c[0] = v->p = 0;
u->fix();
}
}
//====================
Node *access(int u) { return access(node + u); }
void makeRoot(int u) { makeRoot(node + u); }
bool connected(int u, int v) { return connected(node + u, node + v); }
void link(int u, int v) { link(node + u, node + v); }
void cut(int u, int v) { cut(node + u, node + v); }
};
int read() {
int ret = 0;
char c = getchar();
while ('0' > c || c > '9') c = getchar();
while ('0' <= c && c <= '9') {
ret *= 10;
ret += c - '0';
c = getchar();
}
return ret;
}
int n, q, m;
int a[MAX_N];
LCT tr;
int main() {
n = read();
q = read();
for (int i = 1; i <= n; ++i) {
a[i] = i;
}
m = n;
while (q--) {
int u = read(), v = read(), w = read();
if (!tr.connected(u, v)) {
puts("YES");
m += 1;
tr.node[m].isEdge = 1;
tr.node[m].val = w;
tr.link(u, m);
tr.link(v, m);
} else {
tr.makeRoot(u);
tr.access(v);
tr.node[v].splay();
if (tr.node[v].fTot -
(tr.node[v].c[1] ? tr.node[v].c[1]->fTot : 0)) {
puts("NO");
} else if (1 ==
(tr.node[v].tot ^
(tr.node[v].c[1] ? tr.node[v].c[1]->tot : 0) ^ w)) {
puts("YES");
tr.node[v].c[0]->flz = 1;
tr.node[v].c[0]->fTot = tr.node[v].c[0]->eSz;
} else {
puts("NO");
}
}
}
return 0;
}心路历程
想出性质的时候还不会LCT,当时考虑的做法是缩点处理后两个性质
然后写了奇怪的LCT,维护了很多东西,常数巨大,T了
苦思之后在梦里想起有快读这么个东西,赶紧爬起来改了,就过了