wqs二分
概要
这一技巧专门用于解决形式如下的问题
给定若干件物品,从中选出
k件,使其价值和最大
其中关键的限定条件为:
- 最终价值和为按件加和的形式,即无需关心物品价值具体如何,只要总价值为所选物品的和即可
- 在不存在限定条件k的情况下,可以较快得出解(复杂度能再乘log),同时要能顺便求出所取件数
- 满足k与其对应最优解的大小
g(k)所组成的点(k, g(k))落在一上凸包或下凸包上
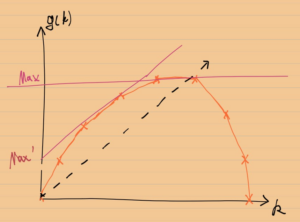
在此基础上我们考虑图像(k,g(k)-ck)(可以考虑为对原坐标轴进行变换)
可以看出新的最大值(即切线截距)将落在凸包上与其相切的一点处,此时限定条件下的最优解将化为全局最优解
即直接将所有物品的价值减去c,再直接进行无限定条件的求解,而后比较所求得的k与限定条件,可判断当前解是否满足限定。
不难想到对c进行二分来进行总的求解
细节
上下界按照需求容易确定
比较麻烦的地方在于,可能存在某些点落在凸包的边而非顶点上,即存在一段连续的k,均满足在某个斜率下值最大,这样可能导致无法求出指定的k
解决思路比较简单,在进行二分求解时,首先确保在选取最大值时优先选更多的物品,随后将收敛条件设为斜率的收敛,只要确保存在符合要求的k,则斜率与变换后最大值的收敛结果必然正确
洛谷P1484 种树
有
n \leq 10^5个坑可以种树,相邻不能种,每个坑都有价值(可为负),求至多种k \leq \frac{n}{2}棵树时的最大价值
做法
显然 O(n) DP可解全局最大值
同时随着选取树的数量的增多,显然最大价值的增量是单调减的,套用wqs二分即可
枚举斜率的时候需要考虑精度问题
AC代码
#include <cmath>
#include <iomanip>
#include <iostream>
using namespace std;
#define int long long
const int MAX_N = 5E5 + 100;
const double INF = 5E11 + 100;
const double eps = 1E-8;
int n, k;
int w[MAX_N];
double dp[MAX_N][2], dpK[MAX_N][2]; //考虑了前k棵树,前一棵是否选了
int curK;
double curGk;
void go(double c) {
dpK[0][0] = dpK[0][1] = 0;
dp[0][0] = 0;
dp[0][1] = -INF;
for (int i = 1; i <= n; ++i) {
if (dp[i - 1][0] > dp[i - 1][1]) {
dp[i][0] = dp[i - 1][0];
dpK[i][0] = dpK[i - 1][0];
} else if (dp[i - 1][0] < dp[i - 1][1]) {
dp[i][0] = dp[i - 1][1];
dpK[i][0] = dpK[i - 1][1];
} else if (dpK[i - 1][0] > dpK[i - 1][1]) {
dp[i][0] = dp[i - 1][0];
dpK[i][0] = dpK[i - 1][0];
} else {
dp[i][0] = dp[i - 1][1];
dpK[i][0] = dpK[i - 1][1];
}
dp[i][1] = dp[i - 1][0] + w[i] - c;
dpK[i][1] = dpK[i - 1][0] + 1;
}
if (dp[n][1] > dp[n][0]) {
curGk = dp[n][1];
curK = dpK[n][1];
} else if (dp[n][1] < dp[n][0]) {
curGk = dp[n][0];
curK = dpK[n][0];
} else if (dpK[n][0] > dpK[n][1]) {
curGk = dp[n][0];
curK = dpK[n][0];
} else {
curGk = dp[n][1];
curK = dpK[n][1];
}
}
signed main() {
ios::sync_with_stdio(false);
cin >> n >> k;
for (int i = 1; i <= n; ++i) {
cin >> w[i];
}
double l = 0, r = INF;
while (fabs(r - l) > eps) {
double mid = (l + r) / 2;
go(mid);
if (curK < k) {
r = mid;
} else {
l = mid;
}
}
cout << fixed << setprecision(0) << curGk + l * k << endl;
return 0;
}